|
Such a polynomial is the univariate eliminant of a polynomial system whose
support is the near circuit which consists of the four integer points
(0,0,0), (1,0,0), (0,1,0), and (1,p,q)
in R3, and the segment
(0,0,0), (0,0,-1), ..., (0,0,-k).
When p and q are relatively prime, the first four vectors
are the vertices of an empty simplex.
The first four points and (0,0,-k) are in convex position
if q-pk-k>0.
We apply the affine transformation
z |---> z + k(1-x-y), and
then set l:=q-pk-k.
When l>0, this point configuration lies in the positive octant.
It is the column vectors of the matrix
| 0 | 0 | 0 | ... | 0 |
1 | 0 | 1 |
| 0 | 0 | 0 | ... | 0 |
0 | 1 | p |
| 0 | 1 | 2 | ... | k |
0 | 0 | l |
and a polynomial system with this support is equivalent to the following system
| x | = | f(z) |
y | = | g(z) |
xy pz lz k
| = | h(z) |
Substituting f(z) for x and g(z) for
y gives the univariate eliminant
f(z)(g(z)) p
z k+l - h(z).
This polynomial makes sense if k+l >=0.
If k+l<0, then we multiply this Laurent polynomial by
z-k-l to turn it into a polynomial.
|
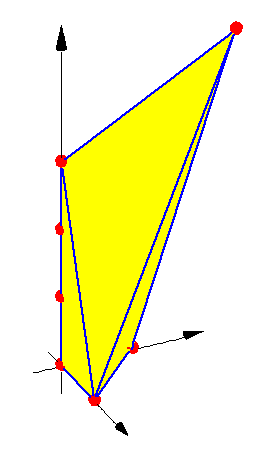
The polytope when
(k, p, l) = (3,2,5).
|
